1.1 What is Mathematics?
Mathematics is, in large part, the search for patterns, and for the explanations as to why those patterns exist. Such patterns indeed exist all around us — in nature, in our homes and schools, and in the motion of the sun, moon, and stars. They occur in everything that we do and see, from shopping and cooking, to throwing a ball and playing games, to understanding weather patterns and using technology. The search for patterns and their explanations can be a fun and creative endeavour. It is for this reason that mathematicians think of mathematics both as an art and as a science. This year, we hope that you will get a chance to see the creativity and artistry involved in discovering and understanding mathematical patterns. It is important to keep in mind that mathematics aims to not just find out what patterns exist, but also the explanations for why they exist. Such explanations can often then be used in applications well beyond the context in which they were discovered, which can then help to propel humanity forward For example, the understanding of patterns in the motion of stars, planets, and their satellites led humankind to develop the theory of gravitation, allowing us to launch our own satellites and send rockets to the Moon and to Mars; similarly, understanding patterns in genomes has helped in diagnosing and curing diseases — among thousands of other such examples. Figure it Out 1. Can you think of other examples where mathematics helps us in our everyday lives? 2. How has mathematics helped propel humanity forward? (You might think of examples involving: carrying out scientific experiments; running our economy and democracy; building bridges, houses or other complex structures; making TVs, mobile phones, computers, bicycles, trains, cars, planes, calendars, clocks, etc.)
Figure it Out
- Can you think of other examples where mathematics helps us in our everyday lives?
- Budgeting and Financial Planning: Mathematics helps us manage money, calculate expenses, savings, and taxes.
- Cooking: Recipes require measurements, ratios, and conversions, all of which involve mathematics.
- Shopping: Mathematics is used to calculate discounts, taxes, and total costs.
- Sports: Mathematics helps in analyzing player statistics, game strategies, and scoring.
- Navigation: GPS systems use mathematical calculations to determine routes and distances.
- Health Monitoring: Devices like fitness trackers use algorithms to calculate steps, calories burned, and heart rate.
- How has mathematics helped propel humanity forward?
Mathematics has been fundamental to countless advancements, including:- Scientific Experiments: Calculations and statistical models are used to design experiments, analyze results, and predict outcomes.
- Economy and Democracy: Economic models, election polling, and resource distribution rely on mathematical principles.
- Engineering and Construction: Building bridges, skyscrapers, and other structures requires geometry, calculus, and physics.
- Technology Development: The creation of TVs, mobile phones, computers, and other devices involves mathematical concepts like algorithms and binary code.
- Transportation: Designing bicycles, trains, cars, and airplanes involves aerodynamics, mechanics, and geometry.
- Space Exploration: Mathematics allows for calculating satellite trajectories, rocket propulsion, and space navigation.
- Timekeeping: Calendars and clocks rely on mathematical patterns of time measurement.
In each case, mathematics serves as the foundation for understanding, creating, and innovating systems and tools that improve daily life and drive progress.
1.2 Patterns in Numbers
Among the most basic patterns that occur in mathematics are patterns of numbers, particularly patterns of whole numbers: 0, 1, 2, 3, 4, … The branch of Mathematics that studies patterns in whole numbers is called number theory. Number sequences are the most basic and among the most fascinating types of patterns that mathematicians study. Table 1 shows some key number sequences that are studied in Mathematics.
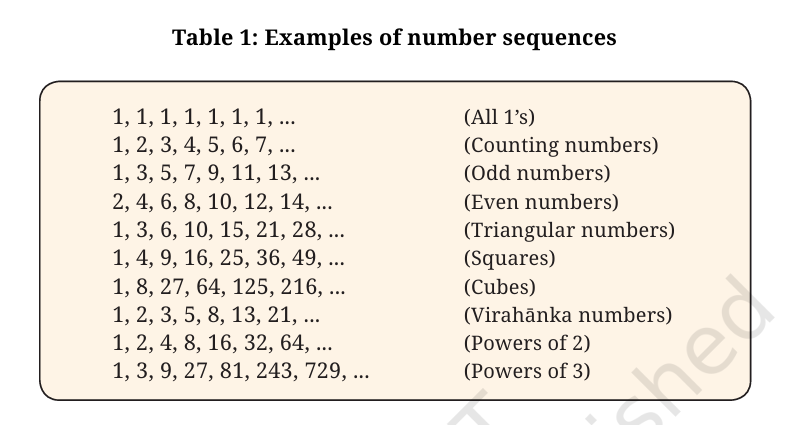
Figure it Out
- Can you recognize the pattern in each of the sequences in Table 1?
Yes, each sequence follows a specific rule or pattern, such as constant values, arithmetic progression, geometric progression, or other mathematical formulas.
- Rewrite each sequence of Table 1 with the next three numbers, and explain the rule for forming them:
| Sequence | Extended Sequence | Rule |
|---|---|---|
| 1, 1, 1, 1, 1, 1, 1, … | 1, 1, 1, 1, 1, 1, 1, 1, 1, … | All numbers are the same (1) in this sequence. |
| 1, 2, 3, 4, 5, 6, 7, … | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 | Counting numbers, formed by adding 1 to the previous number. |
| 1, 3, 5, 7, 9, 11, 13, … | 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 | Odd numbers, formed by adding 2 to the previous number. |
| 2, 4, 6, 8, 10, 12, 14, … | 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 | Even numbers, formed by adding 2 to the previous number. |
| 1, 3, 6, 10, 15, 21, 28, … | 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 | Triangular numbers, formed by adding consecutive integers (1, 2, 3, 4, …) to the previous number. |
| 1, 4, 9, 16, 25, 36, 49, … | 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 | Square numbers, formed by squaring the position number (n²). |
| 1, 8, 27, 64, 125, 216, … | 1, 8, 27, 64, 125, 216, 343, 512, 729 | Cube numbers, formed by cubing the position number (n³). |
| 1, 2, 3, 5, 8, 13, 21, … | 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 | Fibonacci (Virahānka) sequence, where each number is the sum of the previous two numbers. |
| 1, 2, 4, 8, 16, 32, 64, … | 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 | Powers of 2, formed by multiplying the previous number by 2. |
| 1, 3, 9, 27, 81, 243, 729, … | 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683 | Powers of 3, formed by multiplying the previous number by 3. |
By identifying and understanding these patterns, we can predict future numbers and appreciate the structure within number sequences.
1.3 Visualising Number Sequences
Many number sequences can be visualised using pictures. Visualising
mathematical objects through pictures or diagrams can be a very
fruitful way to understand mathematical patterns and concepts.
Let us represent the first seven sequences in Table 1 using the
following pictures.
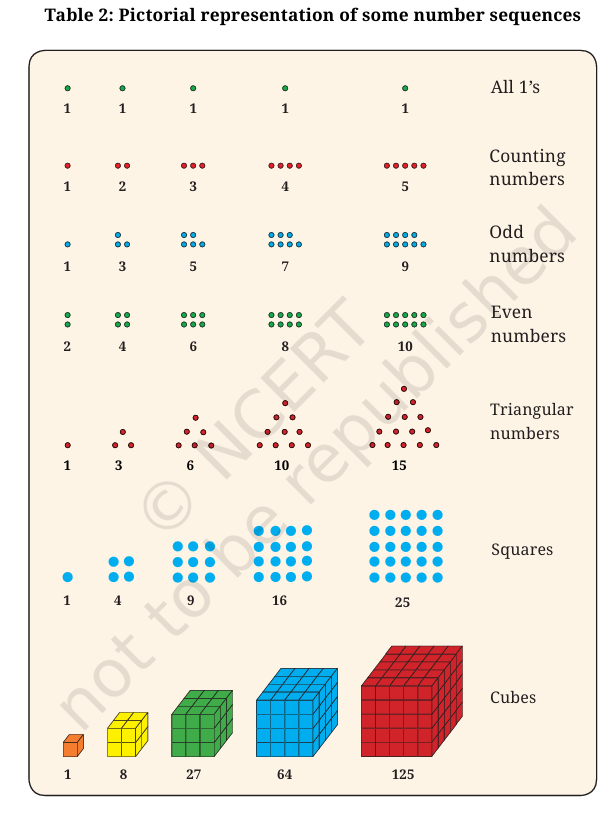
Figure it Out
1. Copy the pictorial representations of the number sequences
in Table 2 in your notebook, and draw the next picture for
each sequence!
2. Why are 1, 3, 6, 10, 15, … called triangular numbers? Why
are 1, 4, 9, 16, 25, … called square numbers or squares?
Why are 1, 8, 27, 64, 125, … called cubes?
3. You will have noticed that 36 is both a triangular number and a
square number! That is, 36 dots can be arranged perfectly both
in a triangle and in a square. Make pictures in your notebook
illustrating this!
This shows that the same number can be represented differently,
and play different roles, depending on the context. Try
representing some other numbers pictorially in different ways!
4. What would you call the following sequence of numbers?
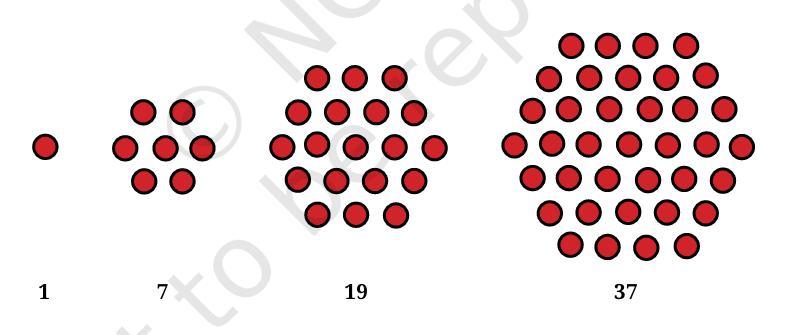
That’s right, they are called hexagonal numbers! Draw these in
your notebook. What is the next number in the sequence?
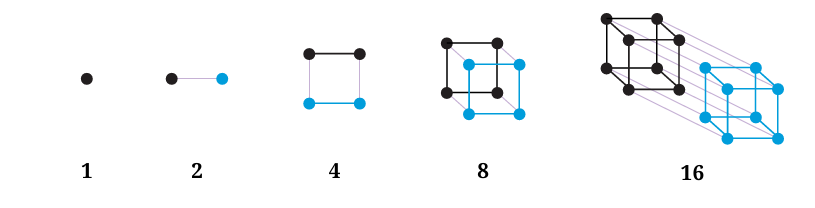
5. Can you think of pictorial ways to visualise the sequence of
Powers of 2? Powers of 3?
Here is one possible way of thinking about Powers of 2:
Answers
1. Copy the pictorial representations of the number sequences and draw the next picture for each sequence.
Copy the given pictures from Table 2 into your notebook, and for each sequence, extend the pattern by drawing the next picture. For example:
- All 1’s: Continue with a single dot.
- Counting numbers: Add one more dot to the row to represent the next number.
- Odd numbers: Add dots to form the next odd number.
- Even numbers: Add dots to form the next even number.
- Triangular numbers: Add an additional row of dots to form the next triangular number.
- Squares: Extend the square by adding another layer of dots.
- Cubes: Extend the cube representation by adding a layer in three dimensions.
2. Why are 1, 3, 6, 10, 15, … called triangular numbers? Why are 1, 4, 9, 16, 25, … called square numbers? Why are 1, 8, 27, 64, 125, … called cubes?
- Triangular Numbers:
These numbers represent dots arranged in the shape of a triangle. Each row of the triangle has one more dot than the previous row. For example:- 1 dot (row 1), 3 dots (rows 1 + 2), 6 dots (rows 1 + 2 + 3), etc.
- Square Numbers:
These numbers represent dots arranged in the shape of a square. Each number corresponds to the total number of dots in a square with equal rows and columns. For example:- 1 dot (1×1), 4 dots (2×2), 9 dots (3×3), etc.
- Cubes:
These numbers represent dots arranged in the shape of a cube in three dimensions. Each number corresponds to the total number of smaller cubes in a larger cube. For example:- 1 cube (1×1×1), 8 cubes (2×2×2), 27 cubes (3×3×3), etc.
3. Why is 36 both a triangular number and a square number? Illustrate this with pictures.
- Triangular Number:
Arrange 36 dots in a triangle with rows increasing by one dot each time (1, 2, 3, …). It forms a perfect triangular arrangement. - Square Number:
Arrange 36 dots in a 6×6 grid, forming a perfect square.
Illustration:
In your notebook, draw a triangle with 36 dots (using rows of 1, 2, 3… adding up to 36) and a square with 36 dots (6 rows and 6 columns).
4. What would you call the following sequence of numbers: 1, 7, 19, 37? What is the next number in the sequence?
- These are hexagonal numbers.
Hexagonal numbers are formed by arranging dots in the shape of a hexagon. - Next Number in the Sequence:
The difference between consecutive numbers in the sequence is 6, 12, 18, etc. (incrementing by 6 each time).- 37 + 30 = 67.
Next number: 67.
- 37 + 30 = 67.
Illustration: Draw hexagonal shapes for 1, 7, 19, 37, and 67 in your notebook.
5. Can you think of pictorial ways to visualize the sequence of Powers of 2 and Powers of 3?
- Powers of 2:
Visualize as doubling squares:- 1 dot → 2 dots → 4 dots arranged in a 2×2 square → 8 dots in two 2×2 squares → 16 dots in a 4×4 square, and so on.
- Powers of 3:
Visualize as cubes:- 1 dot → 3 dots → 9 dots in a 3×3 grid → 27 dots in a 3×3×3 cube, and so on.
Illustration:
In your notebook, draw squares for Powers of 2 and cubes for Powers of 3, showing the exponential growth visually.
Summary of Activities:
- Recreate and extend the given number patterns pictorially.
- Use your notebook to visualize triangular, square, and hexagonal numbers.
- Explore Powers of 2 and 3 with diagrams to understand exponential growth.
1.4 Relations among Number Sequences
Sometimes, number sequences can be related to each other in
surprising ways.
Example: What happens when we start adding up odd numbers?
1 = 1
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
1 + 3 + 5 + 7 + 9 + 11 = 36
.
.
.
This is a really beautiful pattern!
Why does this happen? Do you think it will happen forever?
The answer is that the pattern does happen forever. But why?
As mentioned earlier, the reason why the pattern happens is just as
important and exciting as the pattern itself.
A picture can explain it
Visualising with a picture can help explain the phenomenon. Recall
that square numbers are made by counting the number of dots in a
square grid.
How can we partition the dots in a square grid into odd
numbers of dots: 1, 3, 5, 7,… ?
Think about it for a moment before reading further!
Here is how it can be done:
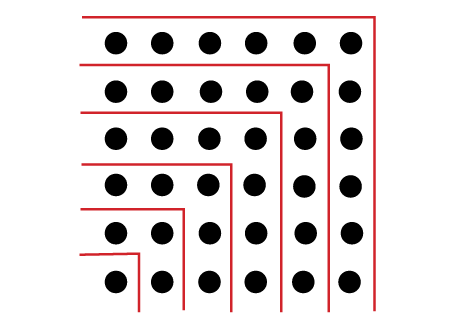
This picture now makes it evident that
1 + 3 + 5 + 7 + 9 + 11 = 36.
Because such a picture can be made for a square of any size, this
explains why adding up odd numbers gives square numbers.
By drawing a similar picture, can you say what is the sum of the
first 10 odd numbers?
Now by imagining a similar picture, or by drawing it partially, as
needed, can you say what is the sum of the first 100 odd numbers?
Another example of such a relation between sequences:
Adding up and down
Let us look at the following pattern:
1 = 1
1 + 2 + 1 = 4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36
.
.
.
This seems to be giving yet another way of getting the square numbers—
by adding the counting numbers up and then down!
Can you find a similar pictorial explanation?

Figure it Out
1. Can you find a similar pictorial explanation for why adding
counting numbers up and down, i.e., 1, 1 + 2 + 1, 1 + 2 + 3 +
2 + 1, …, gives square numbers?
2. By imagining a large version of your picture, or drawing
it partially, as needed, can you see what will be the value of
1 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1?
3. Which sequence do you get when you start to add the All 1’s
sequence up? What sequence do you get when you add the All 1’s
sequence up and down?
4. Which sequence do you get when you start to add the counting
numbers up? Can you give a smaller pictorial explanation?
5. What happens when you add up pairs of consecutive triangular
numbers? That is, take 1 + 3, 3 + 6, 6 + 10, 10 + 15, … Which sequence
do you get? Why? Can you explain it with a picture?
6. What happens when you start to add up powers of 2 starting with
1, i.e., take 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, … ? Now add 1 to each
of these numbers — what numbers do you get? Why does this
happen?
7. What happens when you multiply the triangular numbers by 6
and add 1? Which sequence do you get? Can you explain it with a
picture?
8. What happens when you start to add up hexagonal numbers, i.e.,
take 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37, … ? Which sequence do you
get? Can you explain it using a picture of a cube?
9. Find your own patterns or relations in and among the sequences
in Table 1. Can you explain why they happen with a picture or
otherwise?
Figure it Out
1. Pictorial Explanation for Adding Counting Numbers Up and Down
When adding counting numbers up and down (e.g., 11, 1+2+11 + 2 + 1, 1+2+3+2+11 + 2 + 3 + 2 + 1, etc.), the numbers form symmetrical rows. The sum creates a square grid, similar to the pattern seen with odd numbers.
For example:
- 1+2+3+2+1=91 + 2 + 3 + 2 + 1 = 9: Visualize this as a square grid with 3 rows and 3 columns.
- 1+2+3+4+3+2+1=161 + 2 + 3 + 4 + 3 + 2 + 1 = 16: This forms a 4×4 square grid.
By arranging the dots in rows increasing and then decreasing, the total forms a perfect square.
2. Sum of 1+2+3+…+99+100+99+…+3+2+11 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1
To calculate this sum:
- The sequence is symmetric, so it can be divided into two halves: 1+2+3+…+1001 + 2 + 3 + … + 100 and 99+98+…+199 + 98 + … + 1.
- The sum of 1+2+3+…+1001 + 2 + 3 + … + 100 is calculated as: S=n(n+1)2=100(100+1)2=5050S = \frac{n(n+1)}{2} = \frac{100(100+1)}{2} = 5050
- Adding the second half gives: 5050+5050=101005050 + 5050 = 10100
So, the total sum is 10100.
3. Sequences When Adding the All 1’s Sequence
- Adding All 1’s (up): This forms the counting numbers (1,1+1=2,1+1+1=3,…1, 1+1=2, 1+1+1=3, …).
- Adding All 1’s (up and down): This forms the odd numbers (1,1+1+1=3,1+1+1+1+1=5,…1, 1+1+1=3, 1+1+1+1+1=5, …).
4. Sequence When Adding the Counting Numbers Up
When adding the counting numbers (1,1+2,1+2+3,…1, 1+2, 1+2+3, …), you get the triangular numbers (1,3,6,10,…1, 3, 6, 10, …).
Pictorial Explanation: Each triangular number forms a triangular arrangement of dots, with each row adding one more dot.
5. Adding Pairs of Consecutive Triangular Numbers
When you add pairs of consecutive triangular numbers (1+3,3+6,6+10,…1+3, 3+6, 6+10, …), the result is the square numbers (4,9,16,25,…4, 9, 16, 25, …).
Explanation with Picture:
Each pair of triangular numbers combines to form a perfect square grid of dots.
6. Adding Powers of 2
- Sequence of Sums: 1,1+2=3,1+2+4=7,1+2+4+8=15,…1, 1+2=3, 1+2+4=7, 1+2+4+8=15, …
These are one less than powers of 2 (1,3,7,15,…1, 3, 7, 15, …). - Adding 1 to Each Sum: When you add 1 to each sum, you get the next power of 2 (2,4,8,16,…2, 4, 8, 16, …).
Why? Each sum of powers of 2 represents one less than doubling the previous total. Adding 1 completes the doubling process.
7. Multiplying Triangular Numbers by 6 and Adding 1
- Multiply triangular numbers (1,3,6,10,15,…1, 3, 6, 10, 15, …) by 6 and add 1:
6×1+1=7,6×3+1=19,6×6+1=37,…6 \times 1 + 1 = 7, 6 \times 3 + 1 = 19, 6 \times 6 + 1 = 37, … - The result is the sequence of hexagonal numbers (7,19,37,…7, 19, 37, …).
Explanation with Picture: These numbers can be visualized as dots forming hexagons.
8. Adding Hexagonal Numbers
Adding hexagonal numbers (1,1+7=8,1+7+19=27,…1, 1+7=8, 1+7+19=27, …) results in the cubic numbers (1,8,27,64,…1, 8, 27, 64, …).
Explanation with Picture: Hexagonal numbers can be visualized as layers forming a cube.
9. Find Your Own Patterns Among Sequences
Example of a New Pattern:
- The sum of the first nn square numbers (1,4,9,16,…1, 4, 9, 16, …) equals the formula: S=n(n+1)(2n+1)6S = \frac{n(n+1)(2n+1)}{6}
Why? Visualize square numbers as stacked layers of dots forming a 3D pyramid shape.
1.5 Patterns in Shapes
Other important and basic patterns that occur in Mathematics
are patterns of shapes. These shapes may be in one, two, or three
dimensions (1D, 2D, or 3D) — or in even more dimensions. The
branch of Mathematics that studies patterns in shapes is called
geometry.
Shape sequences are one important type of shape pattern that
mathematicians study. Table 3 shows a few key shape sequences
that are studied in Mathematics
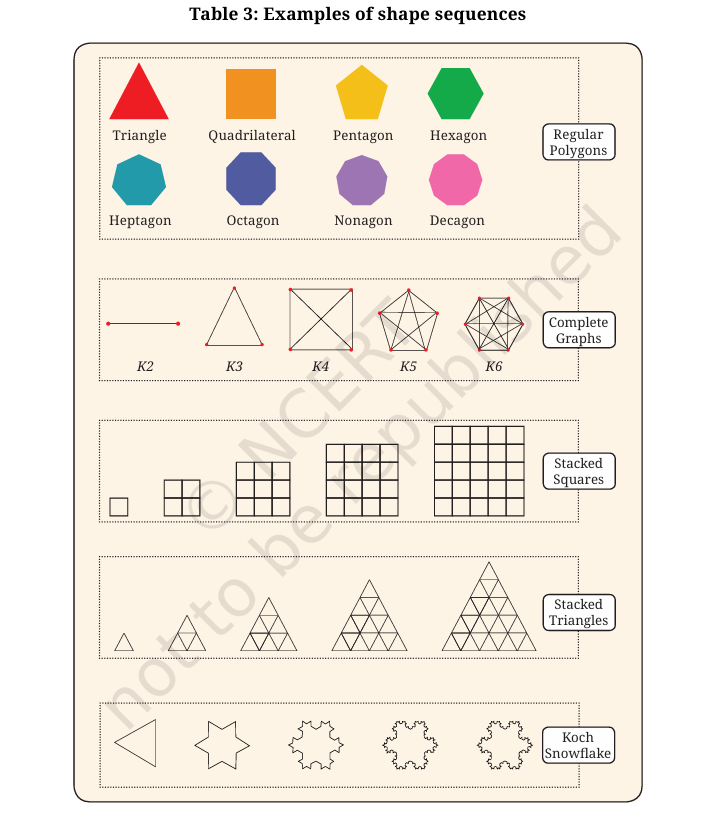
Figure it Out
1. Can you recognize the pattern in each of the sequences in Table 3?
Yes, each sequence in Table 3 follows a specific pattern:
- Regular Polygons (Triangle, Quadrilateral, Pentagon, Hexagon, Heptagon, Octagon, Nonagon, Decagon):
These are polygons with equal sides and angles. The number of sides increases by 1 in each step: 3 sides (triangle), 4 sides (quadrilateral), 5 sides (pentagon), and so on. - Complete Graphs (K2, K3, K4, K5, K6):
These are graphs where every vertex is connected to every other vertex. KnK_n indicates nn vertices. The number of edges grows as n(n−1)2\frac{n(n-1)}{2}. - Stacked Squares:
Squares are stacked one above the other, forming layers. The sequence shows increasing layers of squares. - Stacked Triangles:
Triangles are stacked on top of each other in layers, forming a triangular pyramid-like structure. - Koch Snowflake:
This is a fractal pattern where each line segment is divided into three equal parts, and the middle part is replaced with an outward-pointing equilateral triangle. With each iteration, the complexity increases.
2. Redraw each sequence in your notebook and draw the next shape in each sequence.
- Regular Polygons:
After the decagon (10 sides), the next shape in the sequence would be an 11-sided polygon (Hendecagon). The rule is to increase the number of sides by 1 in each step. - Complete Graphs:
After K6 (6 vertices, fully connected), the next shape would be K7, which has 7 vertices with every vertex connected to the other, forming 7(7−1)2=21\frac{7(7-1)}{2} = 21 edges. The rule is to increase the number of vertices by 1 and connect all vertices. - Stacked Squares:
Add another square layer above the last one. The rule is to keep stacking squares, increasing the height by 1 square in each step. - Stacked Triangles:
Add another triangular layer to the pyramid. The rule is to stack one more triangle on top, increasing the number of triangles in each layer. - Koch Snowflake:
After the current iteration, add a smaller equilateral triangle on the middle of each segment of the current shape. The rule is to divide each line segment into three parts and add a triangle to the middle segment, repeating this process for every segment.
Explanation of Patterns and Rules:
- Regular Polygons:
Each shape is a polygon with an increasing number of sides (triangle = 3 sides, quadrilateral = 4 sides, etc.). - Complete Graphs:
A graph where every vertex is connected to all other vertices. Each step adds one more vertex, increasing the number of edges exponentially. - Stacked Squares:
Squares are added in layers, creating a tower-like structure. - Stacked Triangles:
Triangles are stacked in layers, forming a triangular pyramid structure. - Koch Snowflake:
A fractal pattern is created by repeatedly replacing each line segment with four smaller segments, forming new triangles at each iteration.
1.6 Relation to Number Sequences
Often, shape sequences are related to number sequences in
surprising ways. Such relationships can be helpful in studying and
understanding both the shape sequence and the related number
sequence.
Example: The number of sides in the shape sequence of Regular
Polygons is given by the counting numbers starting at 3, i.e., 3, 4, 5, 6,
7, 8, 9, 10, …. That is why these shapes are called, respectively, regular
triangle, quadrilateral (i.e., square), pentagon, hexagon, heptagon,
octagon, nonagon, decagon, etc., respectively.
The word ‘regular’ refers to the fact that these shapes have
equal-length sides and also equal ‘angles’ (i.e., the sides look the same
and the corners also look the same). We will discuss angles in more
depth in the next chapter.
The other shape sequences in Table 3 also have beautiful
relationships with number sequences.
Figure it Out
1. Count the number of sides and corners in the sequence of Regular Polygons.
- Number of sides:
Regular Polygons have sides corresponding to the sequence of counting numbers starting at 3:
3,4,5,6,7,8,9,10,…3, 4, 5, 6, 7, 8, 9, 10, …. - Number of corners:
Regular Polygons also have the same number of corners as sides:
3,4,5,6,7,8,9,10,…3, 4, 5, 6, 7, 8, 9, 10, ….
Explanation:
Each side of a polygon corresponds to a corner (or vertex) where two sides meet. Therefore, the number of sides equals the number of corners for every regular polygon.
2. Count the number of lines in each shape in the sequence of Complete Graphs.
The sequence is 1, 3, 6, 10, 15, … (Triangular numbers).
Explanation:
A complete graph has all possible connections between nn vertices. The formula counts the total number of unique connections.
3. Count the number of little squares in each shape of the sequence of Stacked Squares.
- Number of squares:
In each layer of Stacked Squares, the number of squares increases as follows:- 1st shape: 12=11^2 = 1
- 2nd shape: 22=42^2 = 4
- 3rd shape: 32=93^2 = 9
- 4th shape: 42=164^2 = 16
The sequence is 1, 4, 9, 16, … (Square numbers).
Explanation:
Each layer forms a perfect square grid with nn rows and nn columns. The total number of small squares equals n2n^2.
4. Count the number of little triangles in each shape of the sequence of Stacked Triangles.
- Number of triangles:
The triangles are stacked in rows, with each row containing one more triangle than the row above:- 1st shape: 1=11 = 1
- 2nd shape: 1+2=31 + 2 = 3
- 3rd shape: 1+2+3=61 + 2 + 3 = 6
- 4th shape: 1+2+3+4=101 + 2 + 3 + 4 = 10
The sequence is 1, 3, 6, 10, … (Triangular numbers).
Explanation:
The number of triangles in each shape corresponds to the sum of the first nn counting numbers, which forms the triangular number sequence.
5. Count the total line segments in the Koch Snowflake sequence.
- Number of line segments:
The number of line segments in the Koch Snowflake grows as follows:- Initial shape (Stage 0): 3 segments (triangle).
- Stage 1: Each segment is divided into 4 smaller segments → 3×4=123 \times 4 = 12.
- Stage 2: Each of the 12 segments is divided into 4 smaller segments → 12×4=4812 \times 4 = 48.
- Stage 3: Each of the 48 segments is divided into 4 smaller segments → 48×4=19248 \times 4 = 192.
The sequence is 3, 12, 48, 192, …, which follows the formula:
Segments=3×4n\text{Segments} = 3 \times 4^n
where nn is the stage of the Koch Snowflake.
Explanation:
Each stage involves replacing every line segment with 4 smaller segments, causing the number of segments to grow exponentially.
Summary of Relationships Between Shapes and Numbers:
- Regular Polygons: Counting numbers for sides and corners.
- Complete Graphs: Triangular numbers for edges.
- Stacked Squares: Square numbers for small squares.
- Stacked Triangles: Triangular numbers for small triangles.
- Koch Snowflake: Exponential growth following 3×4n3 \times 4^n.
These relationships highlight how geometry and number sequences are interconnected.
Summary
Mathematics may be viewed as the search for patterns and for the
explanations as to why those patterns exist.
Among the most basic patterns that occur in mathematics are number
sequences.
Some important examples of number sequences include the counting
numbers, odd numbers, even numbers, square numbers, triangular
numbers, cube numbers, Virahānka numbers, and powers of 2.
Sometimes number sequences can be related to each other in beautiful
and remarkable ways. For example, adding up the sequence of odd
numbers starting with 1 gives square numbers.
Visualising number sequences using pictures can help to understand
sequences and the relationships between them.
Shape sequences are another basic type of pattern in mathematics.
Some important examples of shape sequences include regular polygons,
complete graphs, stacked triangles and squares, and Koch snowflake
iterations. Shape sequences also exhibit many interesting relationships
with number sequences.
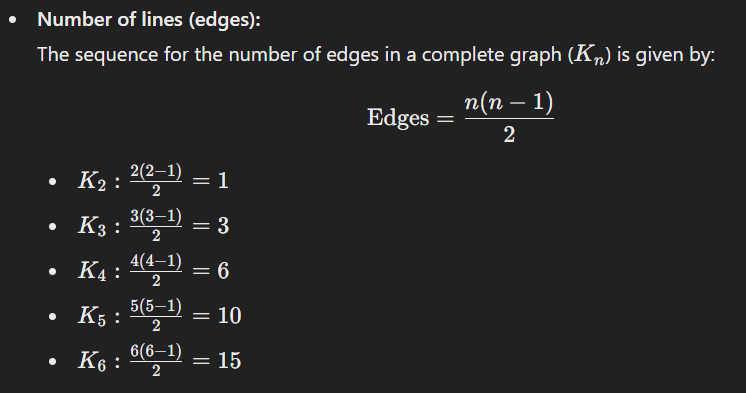
No Responses